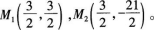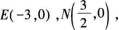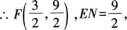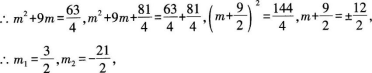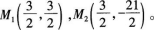(1)由y=0得,似2-2ax-3a=0,∵a≠0,∴x2-2x-3=0,解得X1=-1,X2=3,
∴点A的坐标为(-1,0),点B的坐标为(3,0)。
(2)由y=ax2-2ax-3a,令x=0,得y=-3a,
∴c(0,-3a),又∵y=ax2-2ax-3a=a(x-1)2-4a,得D(1,一4a),∴DH=1,CH=|-4a-(-3a)|=|a|,∴| a|=1。a=-1或1(舍去),∴C(0,3),D(1,4)。
设直线CD的解析式为y=kx+b,把CD两点的坐标代入得

∴直线CD的解析式为y=x+3。
(3)存在。
由(2)得,
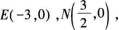
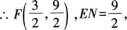
作MQ ⊥CD于Q,
设存在满足条件的点

整理得4m2+36m-63=0,
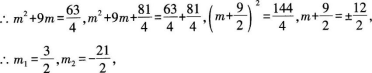
∴点M的坐标为