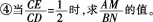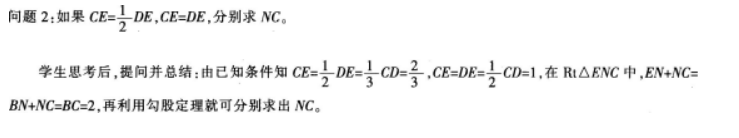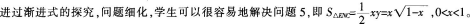(1)本题具有开放性,题目设置合理即可。下面是几个示例: 设正方形纸片△BCD边长为2.
①E在什么位置时,△ENC是一个角为30°的直角三角形;
②试写出NC与EC的数量关系;
③求E在什么位置时,AENC的面积取得最大值;
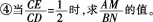
(2)导入:
采用练习导入法,利用一个简单的练习题引入本节课内容。
新课讲授:
根据导入的例题,提出问题:在之前学习的三角形知识中,有哪些常用的性质和定理
预设:①全等三角形判定定理,②相似三角形判定定理,③等腰三角形性质,④勾股定理……
找学生回答并追问,明确具体的性质和定理内容。
在复习之前的知识之后,结合(1)中②③进行“探究式”解题教学。
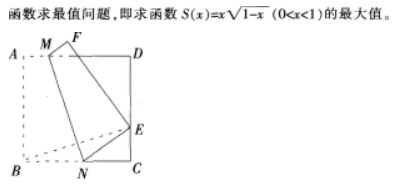
给出例题:如图所示,已知正方形纸片ABCD边长为2,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),压平后得到折痕MN,A点落在点F处。
问题1:根据条件,能够获得哪些结论
学生七嘴八舌地说着,教师提问后总结:AM=FM,BN=EN,Rt△ENC,MN所在的直线是BE的垂直平分线(需连接BE),∠NBE=∠NEB,∠ENC=2N∠BE,……
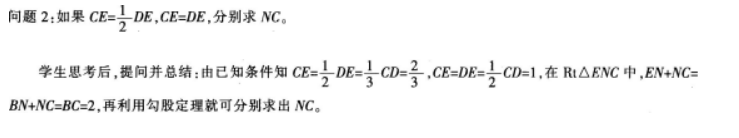
问题3:如果设NC=x,EC=y,试求y关于x的函数关系式。

问题4:在问题3的基础上,我们还能得出什么结论
学生七嘴八舌地说着,教师提问后总结:可以求出Y的取值范围,可以写出△ENC周长和面积的表达式。
问题5:写出△ENC的面积关于x的函数表达式。
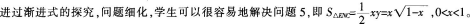
问题6:求E在什么位置时,△ENC的面积取得最大值
之前的几个问题都是为了解决问题6做铺垫的,在前五个问题的基础上研究问题6,几何问题已经转化成
计算部分留给学生。教师对本节课做小结:同学们,我们在学习数学的过程中要善于独立思考,学会在已知条件的基础上归纳概括得出猜想和规律,发现问题、提出问题并想办法去解决问题。要大胆的去尝试,把看起来难的问题,细化成若干个可以解决的小问题,在不断探究不断深入的过程中就会自然而然地解决问题。
作业:已知正方形ABCD边长为2,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),