分析

案例分析题下面是甲、乙两位教师的教学片段。
[教师甲]
教师甲：在平面直角坐标系中，点（x， y）关于y轴的对称点是什么?
学生1：（-x， y）。
教师甲：为了研究函数的对称性，请大家填写下表，观察给定函数的自变量x互为相相反数时，对应的函数值之间具有什么关系?

学生2：通过计算发现，自变量互为相反数时，对应的函数值相等，可以用解析表示，

教师甲：通常我们把具有以上特征的函数称为偶函数，请大家试着给出偶函数的定义。
[教师乙]
教师乙：我们已经研究了函数的单调性，并且用符号语言精确地描述了函数的单调性，今天我们研究函数的其他性质，请大家画出函数f（x）=x2和g（x）= |x|的图象，并观察它们的共同特征。
（通过观察，学生发现这函数的图象都关于y轴对称）
教师乙：类比函数的单调性，你能用符号语言精确地描述“数图象关于y轴对称”这概念吗?
（通过观察，学生发现f（-x）=f（x）.）
教师乙：通常我们把函数上述特征的函数称为偶函数，请大家试着给出偶函数的定义。
问题：
（1）写出偶函数的定义，并简要说明函数奇偶性的作用；（1分）
（2）对甲、乙两位教师的教学进行评价。（10分）

正确答案

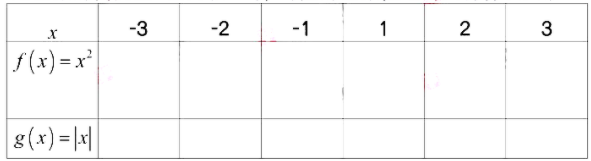
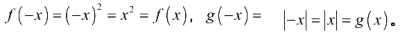（1）偶函数的定义：设函数f（x）的定义域为D，如果Vx∈D，都有-x∈D，且f（-x）=f（x），那么函数f（x）就叫做偶函数。研究奇偶性作用：函数的奇偶性跟其图象的对称性紧密相关，奇函数关于原点对称，偶函数关于y轴对称；有奇偶性的函数只需知道y轴一侧的性质就可推出y轴另一侧的性质，在对函数性质的分析上可以简化运算和分析。
（2）甲教师在对偶函数的新授过程中，着重引导学生通过计算结果分析得到偶函数的定义，缺乏学生主动探索的过程，直接给出本节课的研究主题是对称性，太过于直截了当；而乙教师在教学过程中，引导学生进行了图象观察和结论的探索，更加符合新课改学生是学习主体的理念，并且结合了之前学过的单调性进行导入，在下定义的时候引导学生结合之前学过的知识进行尝试，使学生在学习新知识的同时对旧知识得到很好的巩固。

查看解析

相关试题