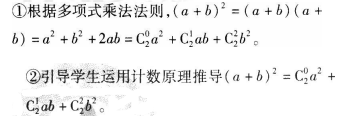(1)看一看以下式子,展开式是什么?有多少项?

通过上面的等式,大家已经发现了一定的规律,展开式的首项和末项的系数均为 1,中间项系数为其“肩上”的两 个数字之和。

那么(a+b)n是否也有这样的规律呢?你能准确写出这些项吗?引出新课。 设计意图:通过这样的导入设计,首先创设情境,激发了学生的学习兴趣以及求知欲,有利于后续课堂的继续推进, 另外在引导的过程中,先从简单的式子人手,再一步步深入,符合学生的认知经验,也为其在后续推导(a+b)n的过 程中提供一定的方法和依据。 (2)推导二项式定理的基本步骤:
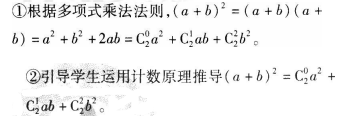
推导思路如下:(a+b)2是 2 个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两个选择,选 a 或选 b,而 且每个(a+b)中的 a 或 b 都选定后,才能得到展开式中的一项。于是由分步乘