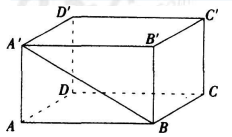
(1)我认为这位老师的教学处理不太妥当。首先,教学活动是师生积极参与,交往互动,共同发 展的过程。教师在提问了两名学生得到答案后。只肯定了乙同学,就进行后续的教学,没有做到面向全体学生,违 背了新课标改革中教育观的要求。其次,在两位同学回答后,只有结果性评价,没有过程性评价,不利于学生形成 良好的学习习惯。最后,针对其中的错误答案,没有引导学生分析错误原因,没有很好地起到组织者、引导者以及 合作者的作用。 (2)①甲同学这种“找不全”的现象可能是由于对异面直线的概念理解不清,导致找不全。教师在日常教学过程中, 应多运用这些学习概念,使学生在认识上获得巩固加深,培养和提高他们运用概念,分析问题和解决问题的能力, 形成新认识结构,同时,要引导学生善于总结,从一个概念出发,把关联概念、派生概念串联成线,相互对比,既 直观形象,又有利于发展学生的创造性思维。如在本题中,教师可以对两条直线平行、相交、异面的三种位置关系 一同研究,相互对照,有利于学生对概念的掌握。 ②甲同学这种“找不全”的现象还可鞥呢是由于解题方法不得当,思维缺少调理性,导致遗漏。针对这一问题,用 条件、结论的改变拓展学生的思维,如提问某个类型的典型题目选择哪一种解法最佳,为什么要选择这种解题方法, 要讲充分,方能让学生真正掌握,还要注意解题方法的比较、总结这一细节,学生才能进一步认识规律。如本题寻 找异面直线的问题,可以转化为寻找共面直线,这样就大幅度地降低了本题目的难度,有利于学生对该知识的理解。